이 번역 페이지는 최신 내용을 담고 있지 않습니다. 최신 내용을 영문으로 보려면 여기를 클릭하십시오.
Optimization Toolbox 튜토리얼
이 튜토리얼에는 fminunc와 fmincon의 두 비선형 최적화 솔버를 사용하는 방법과 옵션을 설정하는 방법을 보여주는 여러 가지 예제가 포함되어 있습니다. 이 튜토리얼에서 설명하는 원리는 fgoalattain, fminimax, lsqnonlin, lsqcurvefit, fsolve 등의 다른 비선형 솔버에도 적용됩니다.
튜토리얼 예제에서는 다음과 같은 작업을 다루게 됩니다.
목적 함수 최소화
추가 파라미터를 포함하는 동일한 함수 최소화
제약 조건이 있는 목적 함수 최소화
기울기 또는 헤세 행렬을 제공하거나 옵션을 변경하여 더욱 효율적이거나 정확한 해 구하기
제약 조건이 없는 최적화 예제
다음과 같은 함수의 최솟값을 구하는 문제를 살펴보겠습니다.
이 함수를 플로팅하면 함수가 최소화되는 지점을 알 수 있습니다.
f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20; fsurf(f,[-2,2],'ShowContours','on')
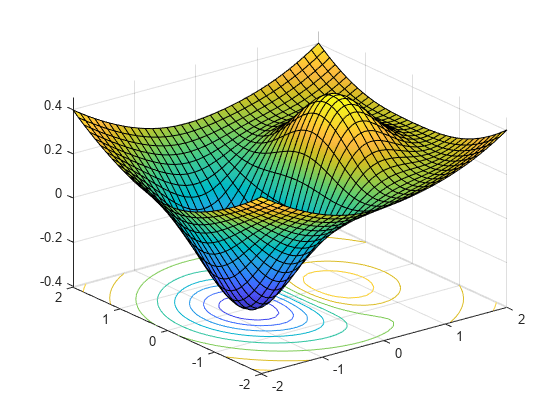
이 플롯은 최솟값이 점 (–1/2,0) 근처에 있음을 보여줍니다.
일반적으로 목적 함수는 MATLAB® 파일로 정의합니다. 이 경우에는 함수가 단순하므로 익명 함수로 정의합니다.
fun = @(x) f(x(1),x(2));
해를 구하기 위한 초기점을 설정합니다.
x0 = [-.5; 0];
fminunc의 디폴트 'quasi-newton' 알고리즘을 사용하기 위한 최적화 옵션을 설정합니다. 이 단계를 거치면 튜토리얼에 나와 있는 예제 코드가 모든 MATLAB 버전에서 동일하게 동작합니다.
options = optimoptions('fminunc','Algorithm','quasi-newton');
솔버가 계산을 수행하는 모든 반복 과정을 표시합니다.
options.Display = 'iter';제약 조건이 없는 비선형 최소화 함수인 fminunc를 호출합니다.
[x, fval, exitflag, output] = fminunc(fun,x0,options);
First-order
Iteration Func-count f(x) Step-size optimality
0 3 -0.3769 0.339
1 6 -0.379694 1 0.286
2 9 -0.405023 1 0.0284
3 12 -0.405233 1 0.00386
4 15 -0.405237 1 3.17e-05
5 18 -0.405237 1 3.35e-08
Local minimum found.
Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.
솔버에서 구한 해를 표시합니다.
uncx = x
uncx = 2×1
-0.6691
0.0000
이 해의 함수 값을 확인합니다.
uncf = fval
uncf = -0.4052
예제에서는 효율성의 척도로 함수 실행 횟수를 사용합니다. 함수의 총 실행 횟수를 확인합니다.
output.funcCount
ans = 18
추가 파라미터를 포함한 제약 조건 없는 최적화 예제
다음으로, 먼저 MATLAB 파일을 사용한 다음 중첩 함수를 사용하여 추가 인수로서 여분의 파라미터를 목적 함수에 전달합니다.
이전 예제에서 설명한 목적 함수를 사용하겠습니다.
다음과 같이 (a,b,c)로 함수를 파라미터화합니다.
이 함수는 원래 목적 함수를 이동하여 크기를 조정한 것입니다.
MATLAB 파일 함수
다음과 같이 정의된 bowlpeakfun이라는 이름의 MATLAB 파일 목적 함수를 살펴보겠습니다.
type bowlpeakfunfunction y = bowlpeakfun(x, a, b, c) %BOWLPEAKFUN Objective function for parameter passing in TUTDEMO. % Copyright 2008 The MathWorks, Inc. y = (x(1)-a).*exp(-((x(1)-a).^2+(x(2)-b).^2))+((x(1)-a).^2+(x(2)-b).^2)/c;
다음과 같이 파라미터를 정의합니다.
a = 2; b = 3; c = 10;
다음과 같이 MATLAB 파일에 대한 익명 함수 핸들을 생성합니다.
f = @(x)bowlpeakfun(x,a,b,c)
f = function_handle with value:
@(x)bowlpeakfun(x,a,b,c)
fminunc를 호출하여 최솟값을 구합니다.
x0 = [-.5; 0]; options = optimoptions('fminunc','Algorithm','quasi-newton'); [x, fval] = fminunc(f,x0,options)
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance.
x = 2×1
1.3639
3.0000
fval = -0.3840
중첩 함수
목적 함수를 중첩 함수로 구현하는 nestedbowlpeak 함수를 살펴보겠습니다.
type nestedbowlpeakfunction [x,fval] = nestedbowlpeak(a,b,c,x0,options)
%NESTEDBOWLPEAK Nested function for parameter passing in TUTDEMO.
% Copyright 2008 The MathWorks, Inc.
[x,fval] = fminunc(@nestedfun,x0,options);
function y = nestedfun(x)
y = (x(1)-a).*exp(-((x(1)-a).^2+(x(2)-b).^2))+((x(1)-a).^2+(x(2)-b).^2)/c;
end
end
파라미터 (a,b,c)는 nestedfun이라는 중첩 목적 함수에서 인식됩니다. 바깥쪽 함수 nestedbowlpeak는 fminunc를 호출하고 목적 함수 nestedfun을 전달합니다.
다음과 같이 파라미터, 초기 추측값, 옵션을 정의합니다.
a = 2; b = 3; c = 10; x0 = [-.5; 0]; options = optimoptions('fminunc','Algorithm','quasi-newton');
최적화를 실행합니다.
[x,fval] = nestedbowlpeak(a,b,c,x0,options)
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance.
x = 2×1
1.3639
3.0000
fval = -0.3840
두 가지 접근법에서 모두 동일한 답이 나오므로, 편의에 맞게 사용하면 됩니다.
제약 조건이 있는 최적화 예제: 부등식
제약 조건이 있는 이전 문제를 살펴보겠습니다.
제약 조건 세트는 기울어진 타원의 내부입니다. 기울어진 타원과 함께 플로팅된 목적 함수의 등고선을 확인합니다.
f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20; g = @(x,y) x.*y/2+(x+2).^2+(y-2).^2/2-2; fimplicit(g) axis([-6 0 -1 7]) hold on fcontour(f) plot(-.9727,.4685,'ro'); legend('constraint','f contours','minimum'); hold off
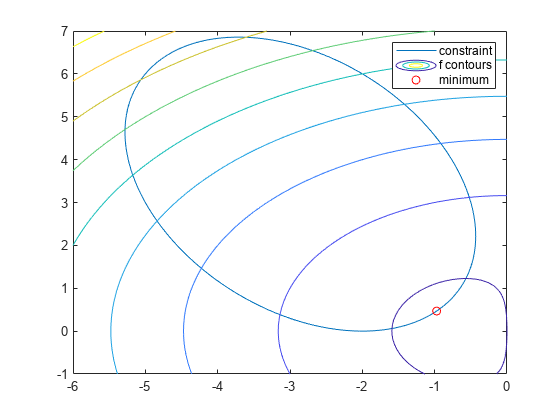
이 플롯은 타원 내부에서 목적 함수의 최솟값이 타원의 오른쪽 아래 부분 주변에 있음을 보여줍니다. 플로팅된 최솟값을 계산하기 전에 해를 추측합니다.
x0 = [-2 1];
interior-point 알고리즘을 사용하고 각 반복 시 결과를 표시하도록 최적화 옵션을 설정합니다.
options = optimoptions('fmincon','Algorithm','interior-point','Display','iter');
솔버를 사용하려면 비선형 제약 조건 함수가 두 개의 출력값, 즉 비선형 부등식에 대한 출력값 하나와 비선형 등식에 대한 출력값 하나를 제공해야 합니다. 두 출력값을 모두 제공하려면 deal 함수를 사용하여 제약 조건을 작성하십시오.
gfun = @(x) deal(g(x(1),x(2)),[]);
제약 조건이 있는 비선형 솔버를 호출합니다. 이 문제에는 선형 등식, 선형 부등식 또는 선형 범위가 없으므로 이러한 인수에 대해서는 [ ]을 전달합니다.
[x,fval,exitflag,output] = fmincon(fun,x0,[],[],[],[],[],[],gfun,options);
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 3 2.365241e-01 0.000e+00 1.972e-01
1 6 1.748504e-01 0.000e+00 1.734e-01 2.260e-01
2 10 -1.570560e-01 0.000e+00 2.608e-01 9.347e-01
3 14 -6.629160e-02 0.000e+00 1.241e-01 3.103e-01
4 17 -1.584082e-01 0.000e+00 7.934e-02 1.826e-01
5 20 -2.349124e-01 0.000e+00 1.912e-02 1.571e-01
6 23 -2.255299e-01 0.000e+00 1.955e-02 1.993e-02
7 26 -2.444225e-01 0.000e+00 4.293e-03 3.821e-02
8 29 -2.446931e-01 0.000e+00 8.100e-04 4.035e-03
9 32 -2.446933e-01 0.000e+00 1.999e-04 8.126e-04
10 35 -2.448531e-01 0.000e+00 4.004e-05 3.289e-04
11 38 -2.448927e-01 0.000e+00 4.036e-07 8.156e-05
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
솔버에서 구한 해를 표시합니다.
x
x = 1×2
-0.9727 0.4686
이 해의 함수 값을 확인합니다.
fval
fval = -0.2449
함수의 총 실행 횟수를 확인합니다.
Fevals = output.funcCount
Fevals = 38
해에서 부등식 제약 조건이 충족되었습니다.
[c, ceq] = gfun(x)
c = -2.4608e-06
ceq =
[]
c(x)가 0에 가까우므로 제약 조건이 활성 상태입니다. 이는 제약 조건이 해에 영향을 미친다는 것을 의미합니다. 제약 조건이 없는 해를 다시 호출합니다.
uncx
uncx = 2×1
-0.6691
0.0000
제약 조건이 없는 목적 함수를 다시 호출합니다.
uncf
uncf = -0.4052
제약 조건으로 인해 해가 얼마나 달라졌으며 목적 함수 값은 얼마나 증가했는지 살펴보십시오.
fval-uncf
ans = 0.1603
제약 조건이 있는 최적화 예제: 사용자 제공 기울기
기울기를 제공하면 최적화 문제를 더 효율적이고 정확하게 풀 수 있습니다. 이전 예제와 마찬가지로, 이 예제에서는 부등식 제약 조건이 있는 문제를 풉니다.
f(x)의 기울기를 fmincon에 제공하기 위해 MATLAB 파일 형식으로 목적 함수를 작성합니다.
type onehumpfunction [f,gf] = onehump(x)
% ONEHUMP Helper function for Tutorial for the Optimization Toolbox demo
% Copyright 2008-2009 The MathWorks, Inc.
r = x(1)^2 + x(2)^2;
s = exp(-r);
f = x(1)*s+r/20;
if nargout > 1
gf = [(1-2*x(1)^2)*s+x(1)/10;
-2*x(1)*x(2)*s+x(2)/10];
end
제약 조건과 해당 기울기는 MATLAB 파일 tiltellipse에 포함되어 있습니다.
type tiltellipsefunction [c,ceq,gc,gceq] = tiltellipse(x)
% TILTELLIPSE Helper function for Tutorial for the Optimization Toolbox demo
% Copyright 2008-2009 The MathWorks, Inc.
c = x(1)*x(2)/2 + (x(1)+2)^2 + (x(2)-2)^2/2 - 2;
ceq = [];
if nargout > 2
gc = [x(2)/2+2*(x(1)+2);
x(1)/2+x(2)-2];
gceq = [];
end
해를 구하기 위한 초기점을 설정합니다.
x0 = [-2; 1];
비교 목적으로 이전 예제에서와 동일한 알고리즘을 사용하도록 최적화 옵션을 설정합니다.
options = optimoptions('fmincon','Algorithm','interior-point');
목적 함수와 제약 조건 함수에서 기울기 정보를 사용하는 옵션을 설정합니다. 참고: 이 옵션은 반드시 설정해야 하며 그렇지 않은 경우 기울기 정보가 무시됩니다.
options = optimoptions(options,... 'SpecifyObjectiveGradient',true,... 'SpecifyConstraintGradient',true);
이번에는 유한 차분을 사용해 기울기를 추정할 필요가 없으므로 fmincon의 함수 실행 횟수가 더 적어야 합니다. 각 반복 시에 결과를 표시하는 옵션을 설정합니다.
options.Display = 'iter';다음과 같이 솔버를 호출합니다.
[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
@tiltellipse,options); First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 1 2.365241e-01 0.000e+00 1.972e-01
1 2 1.748504e-01 0.000e+00 1.734e-01 2.260e-01
2 4 -1.570560e-01 0.000e+00 2.608e-01 9.347e-01
3 6 -6.629161e-02 0.000e+00 1.241e-01 3.103e-01
4 7 -1.584082e-01 0.000e+00 7.934e-02 1.826e-01
5 8 -2.349124e-01 0.000e+00 1.912e-02 1.571e-01
6 9 -2.255299e-01 0.000e+00 1.955e-02 1.993e-02
7 10 -2.444225e-01 0.000e+00 4.293e-03 3.821e-02
8 11 -2.446931e-01 0.000e+00 8.100e-04 4.035e-03
9 12 -2.446933e-01 0.000e+00 1.999e-04 8.126e-04
10 13 -2.448531e-01 0.000e+00 4.004e-05 3.289e-04
11 14 -2.448927e-01 0.000e+00 4.036e-07 8.156e-05
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
이전 예제에서 fmincon이 기울기를 제대로 추정했으므로 이 예제에서의 반복도 유사합니다.
솔버에서 구한 해를 표시합니다.
xold = x
xold = 2×1
-0.9727
0.4686
이 해의 함수 값을 확인합니다.
minfval = fval
minfval = -0.2449
함수의 총 실행 횟수를 확인합니다.
Fgradevals = output.funcCount
Fgradevals = 14
이 횟수를 기울기를 사용하지 않는 경우의 함수 실행 횟수와 비교합니다.
Fevals
Fevals = 38
제약 조건이 있는 최적화 예제: 디폴트 종료 허용오차 변경하기
이 예제에서는 계속해서 기울기를 사용하고 동일한 제약 조건이 적용된 문제를 풉니다.
.
이 경우에는 디폴트 종료 조건(options.StepTolerance 및 options.OptimalityTolerance)을 재정의하여 더 정확한 해를 구할 수 있습니다. fmincon interior-point 알고리즘에 대한 디폴트 값은 options.StepTolerance = 1e-10과 options.OptimalityTolerance = 1e-6입니다.
이러한 두 가지 디폴트 종료 조건을 재정의합니다.
options = optimoptions(options,... 'StepTolerance',1e-15,... 'OptimalityTolerance',1e-8);
다음과 같이 솔버를 호출합니다.
[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
@tiltellipse,options); First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 1 2.365241e-01 0.000e+00 1.972e-01
1 2 1.748504e-01 0.000e+00 1.734e-01 2.260e-01
2 4 -1.570560e-01 0.000e+00 2.608e-01 9.347e-01
3 6 -6.629161e-02 0.000e+00 1.241e-01 3.103e-01
4 7 -1.584082e-01 0.000e+00 7.934e-02 1.826e-01
5 8 -2.349124e-01 0.000e+00 1.912e-02 1.571e-01
6 9 -2.255299e-01 0.000e+00 1.955e-02 1.993e-02
7 10 -2.444225e-01 0.000e+00 4.293e-03 3.821e-02
8 11 -2.446931e-01 0.000e+00 8.100e-04 4.035e-03
9 12 -2.446933e-01 0.000e+00 1.999e-04 8.126e-04
10 13 -2.448531e-01 0.000e+00 4.004e-05 3.289e-04
11 14 -2.448927e-01 0.000e+00 4.036e-07 8.156e-05
12 15 -2.448931e-01 0.000e+00 4.000e-09 8.230e-07
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
새로운 허용오차로 인해 생긴 차이를 더 정확히 보려면 해에 소수 자릿수를 더 표시하십시오.
format long솔버에서 구한 해를 표시합니다.
x
x = 2×1
-0.972742227363546
0.468569289098342
이들 값을 이전 예제의 값들과 비교합니다.
xold
xold = 2×1
-0.972742694488360
0.468569966693330
값의 변화를 확인합니다.
x - xold
ans = 2×1
10-6 ×
0.467124813385844
-0.677594988729435
이 해의 함수 값을 확인합니다.
fval
fval = -0.244893137879894
해가 얼마나 개선되었는지 살펴보십시오.
fval - minfval
ans =
-3.996450220755676e-07
새로운 해가 더 작으므로 결과가 음수입니다.
함수의 총 실행 횟수를 확인합니다.
output.funcCount
ans =
15
이 횟수를 사용자가 제공한 기울기와 디폴트 허용오차로 푼 예제의 함수 실행 횟수와 비교합니다.
Fgradevals
Fgradevals =
14
제약 조건이 있는 최적화 예제: 사용자 제공 헤세 행렬
기울기 외에 헤세 행렬을 제공하면 솔버가 훨씬 더 정확하고 효율적입니다.
fmincon interior-point 알고리즘은 헤세 행렬을 개별 함수(목적 함수의 일부가 아님)로 받습니다. 헤세 행렬 함수 H(x,lambda)는 라그랑주 함수의 헤세 행렬을 실행합니다. fmincon의 interior-point 알고리즘에 대한 헤세 행렬 항목을 참조하십시오.
사용자가 제공하는 헤세 행렬 함수는 솔버에 lambda.ineqnonlin 및 lambda.eqlin 값을 사용하는 방법을 지시하고, 솔버는 이들 값을 계산하게 됩니다.
이 예제에는 부등식 제약 조건이 하나 있으므로, hessfordemo 함수에 지정된 것처럼 헤세 행렬이 정의됩니다.
type hessfordemofunction H = hessfordemo(x,lambda)
% HESSFORDEMO Helper function for Tutorial for the Optimization Toolbox demo
% Copyright 2008-2009 The MathWorks, Inc.
s = exp(-(x(1)^2+x(2)^2));
H = [2*x(1)*(2*x(1)^2-3)*s+1/10, 2*x(2)*(2*x(1)^2-1)*s;
2*x(2)*(2*x(1)^2-1)*s, 2*x(1)*(2*x(2)^2-1)*s+1/10];
hessc = [2,1/2;1/2,1];
H = H + lambda.ineqnonlin(1)*hessc;
헤세 행렬을 사용하기 위해서는 옵션을 다음과 같이 적절히 설정해야 합니다.
options = optimoptions('fmincon',... 'Algorithm','interior-point',... 'SpecifyConstraintGradient',true,... 'SpecifyObjectiveGradient',true,... 'HessianFcn',@hessfordemo);
허용오차가 디폴트 값으로 설정되어 있으므로 함수 실행 횟수가 더 적어야 합니다. 각 반복 시에 결과를 표시하는 옵션을 설정합니다.
options.Display = 'iter';다음과 같이 솔버를 호출합니다.
[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
@tiltellipse,options); First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 1 2.365241e-01 0.000e+00 1.972e-01
1 3 5.821325e-02 0.000e+00 1.443e-01 8.728e-01
2 5 -1.218829e-01 0.000e+00 1.007e-01 4.927e-01
3 6 -1.421167e-01 0.000e+00 8.486e-02 5.165e-02
4 7 -2.261916e-01 0.000e+00 1.989e-02 1.667e-01
5 8 -2.433609e-01 0.000e+00 1.537e-03 3.486e-02
6 9 -2.446875e-01 0.000e+00 2.057e-04 2.727e-03
7 10 -2.448911e-01 0.000e+00 2.068e-06 4.191e-04
8 11 -2.448931e-01 0.000e+00 2.001e-08 4.218e-06
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
결과에는 더 적은 개수의 상이한 반복 횟수가 표시됩니다.
솔버에서 구한 해를 표시합니다.
x
x = 2×1
-0.972742246093537
0.468569316215571
이 해의 함수 값을 확인합니다.
fval
fval = -0.244893121872758
함수의 총 실행 횟수를 확인합니다.
output.funcCount
ans =
11
이 횟수를 사용자가 제공한 기울기와 디폴트 허용오차로 푼 예제의 함수 실행 횟수와 비교합니다.
Fgradevals
Fgradevals =
14
